Many engineers and hobbyist alike are unable to solve the following ‘simple’ problem without assistance of simulation. If you don’t believe me, try it yourself.
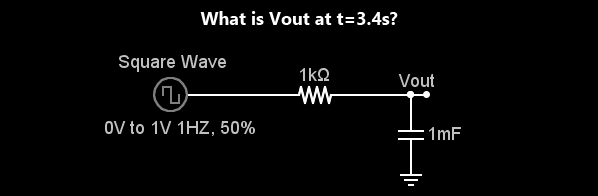
How does one calculate the behavior of a circuit/system with a square wave input? Furthermore, how is this solved on an embedded platform without the aid of a spice simulator like LTSpice? This is relevant question because at times one may be forced to solve/utilize differential equations on embedded systems. This problem may seem awkward since most of academia literature uses a step or impulse as a input as opposed to real-world arbitrary/exogenous input(such as a square wave). In addition, note that neither phasor analysis or Laplace analysis alone is adequate to arrive at a simple solution. However, with their assistance and the Z-transform, one can contrive a simple solution to this problem.
A solution method:
[Disclaimer] As for all problems, many solution methods exist and the following is simply my approach. Step 1, convert the system to the Laplace domain. Step 2, discretize the system and convert it to the Z domain. Step 3, apply the definition of the Z-transform to convert from the discrete frequency domain to the time domain. Step 4, apply the square wave to the resulting function and calculate the answer.
Step 1: Convert circuit to Laplace domain.
First we convert our circuit to the Laplace domain. Capacitors can be re-written as $1/(s \cdot C)$ and inductors (if we had any) are converted to $(s \cdot L)$. Here the values are replaced with their generic counterparts.
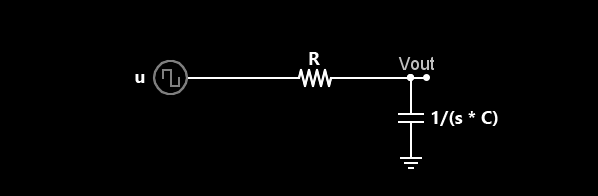
Step 2: Write out the nodal equation.
Writing out the nodal equation for Vout we have the following:
$$\frac{u -V_{out}}{R} = \frac{V_{out} -0}{\frac{1}{s \cdot C}}$$
Now with some algebra one can write the equation in the form of its output and subsequently the transfer function.
$$V_{out} = \frac{u}{1 + s \cdot R \cdot C} $$ $$ H(s) = \frac{1}{1 + s \cdot R \cdot C}$$
Now from here, the traditional approach might be to do the inverse Laplace transform. Often though, this is done for step response or impulse response analysis. You must choose your input ahead of time which eliminates the opportunity to apply any arbitrary input. In addition, the laplace representation of a square wave is tricky to contrive and can be a difficult to invert. Thankfully, a simpler method exists.
Conversion from Laplace domain to Z domain
This is where the long lost friend of the Z-transform comes to the rescue. With the Z transform, one can easily calculate an arbitrary input for a given transfer function. However, how do we convert from the Laplace domain to the Z domain? Note this process is sometimes referred to as system discretization. A simpler method will be provided than what is shown on Wikipedia/Z-transform for conversion. An approximation can be made by considering the numerical derivative and its correlation to the frequency domain.
$$Numerical Derivative = \frac{x(k+1) -x(k)}{\Delta T} $$ $$ Laplace Derivative = s $$ $$ s \approx \frac{z -1}{\Delta T} $$
Note that $\Delta T$ is the sampling period. Now with the approximation of $s$ in terms of $z$, one can substitute it into original transfer function.
$$\frac{Y(k)}{X(k)} = \frac{1}{1 + (\frac{z -1}{\Delta T}) \cdot R \cdot C} $$
Okay thats great, we are in the Z-domain but now how do we go back to a time domain such that we can apply this function? Well again, if you look at Wikipedia for an inverse Z-transform you will see some frighting never used function such as this: $Z^{-1}{X(z)} = \frac{1}{2 \pi j}\oint \limits_{C} X(z)z^{n-1}dz$. However, do not forget the definition of the Z-transform where $z$ is an advance and $z^{-1}$ is a delay of a function. One can apply this definition of the Z-transform after re-arranged and simplification of the original function as seen below.
$$\frac{Y(k)}{X(k)} = \frac{1}{1 + (\frac{z -1}{\Delta T}) \cdot R \cdot C} $$ $$ Y(k) = \frac{\Delta T \cdot X(k)}{\Delta T + (z -1) \cdot R \cdot C} $$ $$ Y(k) \cdot (\Delta T + (z -1) \cdot R \cdot C) = \Delta T \cdot X(k) $$ $$ Y(k) \cdot ((\Delta T -1) + z) \cdot R \cdot C) = \Delta T \cdot X(k) $$
Now if we take into account a realistic sampling period $(\Delta T = 0.01s)$ and that $R \cdot C = 1$, we now have:
$$ Y(k) \cdot (z -0.99) = 0.01 \cdot X(k)$$
Now we apply the definition of the Z-transform and convert back to the discrete time domain. Note the variables change from $ X,Y $ to $ x,y $ which is a common method of annotating the difference between frequency domain and time domain.
$$ y(k+1) = 0.99 \cdot y(k) + 0.01 \cdot x(k) $$ And presto! Here is a function that can easily be programed via C(or your embedded preference) that is in the discrete time domain.
float y = 0.99 * y + 0.01 * x;Next apply the given square wave input to the contrived function. Note the design period was 0.01s so everything is multiplied by a factor of 100.
float y= 0;
int x = 0; //Note sampling rate 100 Hz
for(int i = 1; i <340; i++) //3.4 seconds
{
y = 0.990 * y + 0.01 * x;
x = ((i % 50) == 0) ? (!x) : x; // Square wave of 1Hz
}
printf("Vout = %3.3f V\r\n",y);
//Output: Vout = 0.400 V
Tada, with our 8bit micro-controller or hopefully a 32bit ARM, we are able to calculate what $V_{out}$ is at 3.4 seconds which is $\approx 0.40 V$. Look mom, no simulator! Furthermore, if one puts the values of y in a array and plots it, we get the following:
With that plot, this refresher of Laplace and Z-Transforms comes to a close. Note another method of solving this problem may include a ODE solver or Fourier analysis. However, it is doubtful these methods would production a solution as simple as the Z-transform.
References:
Many thanks to my undergrad controls professor, Dr. Glower, and his easy to follow notes @: http://www.bisonacademy.com/ECE461